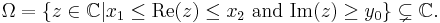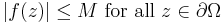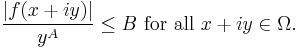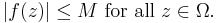Lindelöf's theorem

In mathematics, Lindelöf's theorem is a result in complex analysis named after the Finnish mathematician Ernst Leonard Lindelöf. It states that a holomorphic function on a half-strip in the complex plane that is bounded on the boundary of the strip and does not grow "too fast" in the unbounded direction of the strip must remain bounded on the whole strip. The result is useful in the study of the Riemann zeta function, and is a special case of the Phragmén–Lindelöf principle. Also, see Hadamard three-lines theorem.

Statement of the theorem

Let Ω be a half-strip in the complex plane:

$\Omega = \{ z \in \mathbb{C} | x_1 \leq \mathrm{Re} (z) \leq x_2 \text{ and } \mathrm{Im} (z) \geq y_0 \} \subsetneq \mathbb{C}. \,$

Suppose that ƒ is holomorphic (i.e. analytic) on Ω and that there are constants M, A and B such that

$| f(z) | \leq M \text{ for all } z \in \partial \Omega \,$

and

$\frac{| f (x %2B i y) |}{y^{A}} \leq B \text{ for all } x %2B i y \in \Omega. \,$

Then f is bounded by M on all of Ω:

$| f(z) | \leq M \text{ for all } z \in \Omega. \,$

Edwards, H.M. (2001). Riemann's Zeta Function. New York, NY: Dover. ISBN 0486417409.